Leetcode Problem Solve - Two Sum

Headings

It has been more than a month since I joined the South Korea military. There were a lot of things happened such as the basic training, an additional training unit, and the newly assigned unit. As June 18th of 2024, I have been assigned to Capital Mechanized Infantry Division with Network Management/Operation MOS.

While I have to serve for my country, I will try my best to keep up the programming. This Leetcode solution posts (I will constantly solve) will help me a lot.

Let’s dive in. Shall we?

Introduction

Two Sum Problem Description

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

The Two Sum problem is one of the most famous and straightforward programming questions.

Since it is an easy question, there are not many constraints to consider, although normally they have to be.

Analysis

First, we can naively think that just using the nested loops.

Solutions

1. Nested Loop

Target: 9
[2,7,11,15]
 ^          - The First Loop Pointer
   ^        - The Second Loop Pointer

The idea is extremely simple. Basically, we will try to check every possible solution.

Fortunately, the first case ends in the very first check. However, we should not expect to always be this lucky.

What if the target was 26?

Possible pairs to check: (2,7), (2,11), (2, 15), (7, 11), (7, 15), (11, 15)

We have to check a lot of cases. If the constraint required the result to be in order, it would be more difficult.

So, what is the complexity of the nested loops?

Time Complexity: O(N^2)

Space Complexity: O(1)

def two_sum(nums, target):
    for i in range(len(nums)):
        for j in range(i + 1, len(nums)):
            if nums[i] + nums[j] == target:
                return [i, j]

Follow-up: Can you come up with an algorithm that is less than O(n2) time complexity? Follow-up question from the description

As the follow-up question suggests, the solution can be improved. Think about how you might keep track of the numbers you have seen so far to reduce the number of pairs you need to check.

2. Hashmap

Let’s think about the improvements.

What things we have to consider for the Two Sum question?

1. At least we need to traverse once for the nums array.

The best case would be O(1) as it said, Only one valid answer exists.. Hence, we can terminate the search as soon as we found the valid answer. And, the worst case would be O(N). Becasue of this, we cannot reduce the time complexity below O(N)

2. You can return the answer in any order.

From this, we do not have to traverse back to confirm the right order.

Thus, our plan for now is when we traverse once, we do as many as jobs we can do.

3. We only deal with two numbers to find out the target number.

This is the huge hint. It means that if we know one of the numbers, we know exactly what should we look for the another number to find out the correct answer.

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hash_map = {}  # Create a hash map to store the value and its index
        
        for i, num in enumerate(nums):
            hash_map[num] = i  # Add the current number and its index to the hash map

I started with the very basic code. Traverse the entire nums and add them to the hash_map.

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hash_map = {}  # Create a hash map to store the value and its index
        
        for i, num in enumerate(nums):
            complement = target - num  # Calculate the complement
            hash_map[num] = i  # Add the current number and its index to the hash map
            if complement in hash_map:  # Check if the complement exists in the hash map
                return [hash_map[complement], i]  # Return the indices of the two numbers

Now, we calculate complement by subtracting num from target. Then check the complement does exist in the hash_map or not.

However, this solution has a problem. if the target is an even number and the number you are checking is its exactly half, it will return the same index.

For instance, if the num is [3,2,4] and the target is 6, it will just return [0,0].

We have to check the existence of complement before we modify the hashmap value.

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hash_map = {}  # Create a hash map to store the value and its index
        
        for i, num in enumerate(nums):
            complement = target - num  # Calculate the complement
            
            if complement in hash_map:  # Check if the complement exists in the hash map
                return [hash_map[complement], i]  # Return the indices of the two numbers
            
            hash_map[num] = i  # Add the current number and its index to the hash map

Result

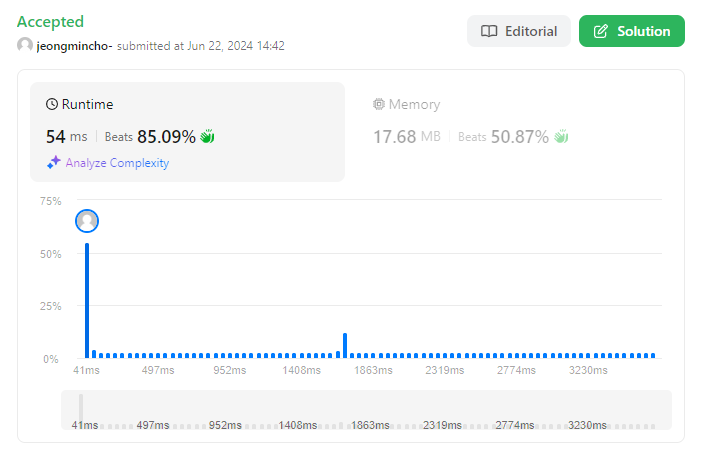
Submission Rresult

The submission was accepted and faster than the most of the submissions.

Time Complexity: O(N)

Space Complexity: O(N)

Conclusion

In this post, we explored two solutions to the Two Sum problem.

We started with a naive nested loop approach and improved it using a hashmap, significantly enhancing the time complexity.

If you have any questions or suggestions, please feel free to leave a comment below.

Thank you for reading!